Titik-titik yang melintasi bidang kuadran koordinat kartesius memainkan peran penting dalam matematika dan ilmu terkait. Ketika kita berbicara tentang menentukan posisi suatu titik pada kuadran ini, hal tersebut melibatkan pemahaman dasar mengenai dua sumbu utama: sumbu X dan sumbu Y. Sederhana, bukan? Namun, keunikan kuadran koordinat terletak pada cara kita menafsirkan lokasi titik tersebut. Sebagai awalan, mari kita telusuri cara kita dapat membaca dan mengartikan posisi suatu titik pada kuadran koordinat. Dengan pemahaman ini, dunia matematika membuka pintu menuju pemecahan masalah yang lebih kompleks.
Menentukan Titik pada Kuadran Koordinat Kartesius
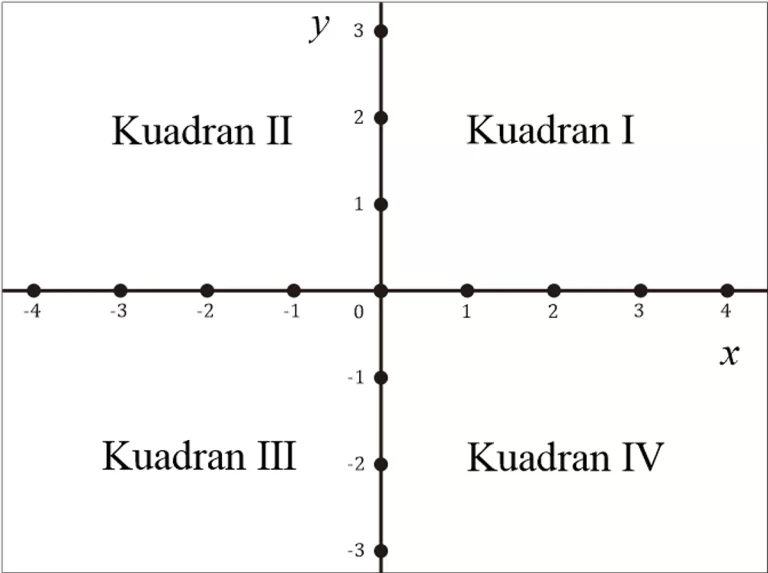
Pengenalan Kuadran Koordinat
Mari kita kenali apa itu kuadran koordinat kartesius. Kuadran koordinat merupakan suatu sistem koordinat dua dimensi yang terdiri dari empat kuadran, dibagi oleh sumbu-x dan sumbu-y. Sumbu-x membentang horizontal, sementara sumbu-y membentang vertikal. Keempat kuadran tersebut diidentifikasi sesuai dengan tanda positif atau negatif dari koordinat titik yang terletak di dalamnya.
Kuadran pertama terletak di sebelah kanan atas, di mana kedua koordinat positif. Kuadran kedua berada di sebelah kiri atas, dengan koordinat negatif pada sumbu-x dan positif pada sumbu-y. Kuadran ketiga berada di sebelah kiri bawah, dengan kedua koordinat negatif. Sementara itu, kuadran keempat terletak di sebelah kanan bawah, dengan koordinat positif pada sumbu-x dan negatif pada sumbu-y.
Cara Membaca Koordinat Titik
Untuk menentukan suatu titik pada kuadran koordinat, perhatikan letak titik tersebut terhadap sumbu-x dan sumbu-y. Misalnya, titik berarti titik tersebut terletak 2 satuan di sepanjang sumbu-x dan 3 satuan di sepanjang sumbu-y. Jika salah satu koordinatnya negatif, seperti , artinya titik berada 1 satuan di sepanjang sumbu-x ke kiri dan 4 satuan di sepanjang sumbu-y ke atas.
Signifikansi Kuadran dalam Analisis Grafik
Signifikansi dari kuadran koordinat ini terletak pada analisis grafik dan representasi visual data. Dengan menempatkan titik-titik pada kuadran, kita dapat melihat pola-pola hubungan antar variabel atau perubahan seiring waktu. Misalnya, pertumbuhan pendapatan sepanjang tahun dapat divisualisasikan dengan titik-titik pada grafik, dan kuadran membantu kita melihat arah dan kecenderungan perubahan tersebut.
Mengapa Menentukan Kuadran Penting
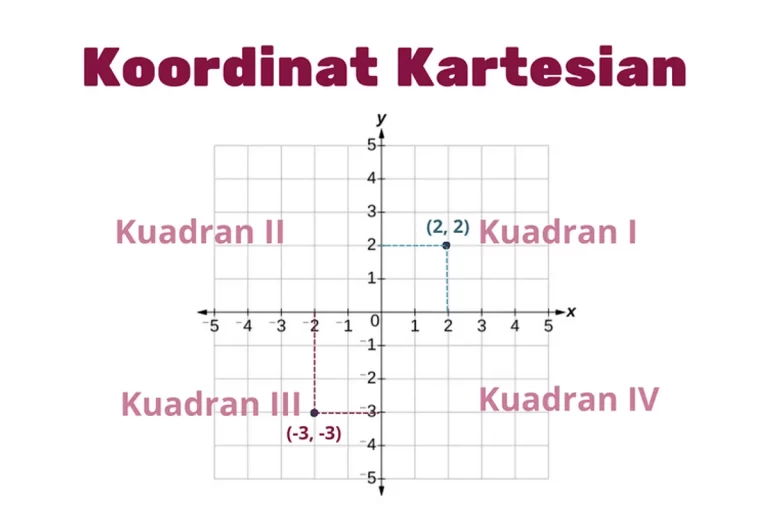
Ketika kita memasuki dunia matematika, pertanyaan mengapa kita perlu menentukan kuadran pada sistem koordinat kartesius mungkin terlintas. Namun, pemahaman tentang kuadran ini menjadi kunci untuk membaca dan menafsirkan informasi dalam grafik atau diagram. Dengan menentukan kuadran, kita dapat dengan cepat mengetahui posisi relatif suatu titik, memudahkan analisis data, dan memberikan dasar yang solid untuk menyusun informasi visual.
Kaitan Antara Kuadran dan Lokasi Titik
Setiap kuadran pada koordinat kartesius memiliki ciri khas dan makna tertentu. Misalnya, kuadran I terletak di sebelah kanan atas, dan titik di kuadran ini memiliki nilai positif pada kedua sumbu. Kuadran II berada di sebelah kiri atas dengan nilai X negatif dan nilai Y positif.
Analisis Data Menggunakan Kuadran Koordinat
Dalam analisis data, kemampuan untuk menempatkan titik pada kuadran menjadi krusial. Sebagai contoh, pada grafik fungsi matematika, kita dapat dengan mudah melihat di mana suatu nilai berada dan bagaimana nilainya berkaitan dengan variabel lain. Dengan kuadran, kita dapat melihat tren, pola, dan anomali data dengan lebih efisien. Pemahaman ini menjadi dasar penting dalam membuat keputusan berdasarkan informasi visual.
Keuntungan Menentukan Kuadran pada Grafik
Menentukan kuadran pada grafik memberikan keuntungan praktis. Kita dapat dengan cepat mengidentifikasi apakah suatu titik berada di kuadran positif atau negatif, serta apakah perubahan nilai variabel bersifat positif atau negatif. Hal ini mempermudah interpretasi grafik, membantu pengambilan keputusan yang lebih tepat, dan meningkatkan efisiensi komunikasi visual dalam konteks data.
Langkah-langkah Menentukan Titik pada Kuadran Koordinat
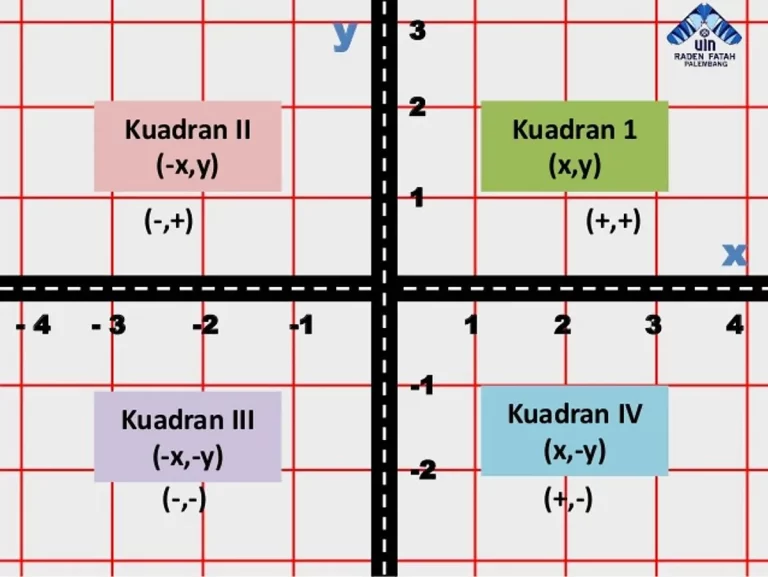
Ketika kita memasuki dunia kuadran koordinat, tak perlu khawatir bingung. Mari kita bersama-sama melangkah dalam petunjuk sederhana untuk menentukan titik pada kuadran koordinat yang kadang terlihat kompleks namun sebenarnya cukup ramah.
Menentukan Koordinat X dan Y
Mari kita mulai langkah yaitu menentukan koordinat X dan Y suatu titik. Koordinat X menunjukkan posisi horizontal, sedangkan koordinat Y menunjukkan posisi vertikal. Bayangkan sumbu X sebagai jalanan lebar, sedangkan sumbu Y adalah jalan setinggi langit. Titik yang kita cari akan bersua dengan garis ini di titik temu yang disebut koordinat.
Langkahnya cukup sederhana, perhatikan seberapa jauh ke kanan atau ke kiri titik dari titik pusat . Begitu juga dengan seberapa tinggi atau rendah dari pusat pada sumbu Y.
Mengenali Positif dan Negatif pada Sumbu
Sumbu X dan Y memiliki keunikan sendiri. Sumbu X dibagi menjadi dua bagian, positif di sebelah kanan titik pusat dan negatif di sebelah kiri. Sementara sumbu Y memiliki positif di atas titik pusat dan negatif di bawahnya. Mengenali ini akan membantu kita memahami posisi suatu titik dengan cepat. Sebagai contoh, jika kita memiliki koordinat , itu berarti kita bergerak tiga langkah ke kanan dari pusat dan dua langkah ke bawah.
Penerapan pada Contoh Grafik
Mari terapkan pengetahuan kita pada contoh grafik. Bayangkan grafik dengan sumbu X dan Y, titik pusat di tengahnya. Jika kita punya titik dengan koordinat , kita tahu itu berada di kuadran kanan atas karena nilai X positif dan nilai Y positif .
Peran Kuadran Koordinat dalam Matematika dan Ilmu Terapan
Kuadran koordinat kartesius, sering dianggap sebagai peta matematika, membawa konsep posisi dan hubungan antar titik. Ini bukan hanya alat matematika, tetapi fondasi bagi banyak ilmu terapan.
Pemanfaatan Kuadran dalam Fisika
Dalam fisika, kuadran koordinat menjadi nakhoda navigasi ruang. Misalnya, saat menganalisis gerak benda, titik pada kuadran membantu merinci arah dan magnitudo gerakan. Oleh karena itu, fisikawan sering "melacak" pergerakan objek menggunakan kuadran ini.
Kalkulasi Matematika dengan Menggunakan Kuadran
Matematika murni memanfaatkan kuadran untuk menghitung sejumlah besar konsep. Ketika melakukan operasi matematika, kuadran memberikan konteks yang jelas, membantu siswa dan profesional memvisualisasikan solusi. Ini adalah alat yang tak tergantikan dalam menyelesaikan persamaan dan pertidaksamaan.
Aplikasi Praktis di Berbagai Bidang
Selain ilmu murni, kuadran koordinat diterapkan di berbagai bidang. Dalam pemrograman komputer, pengembang menggunakan kuadran untuk menetapkan
Hasil dan Interpretasi Grafik Kuadran Koordinat
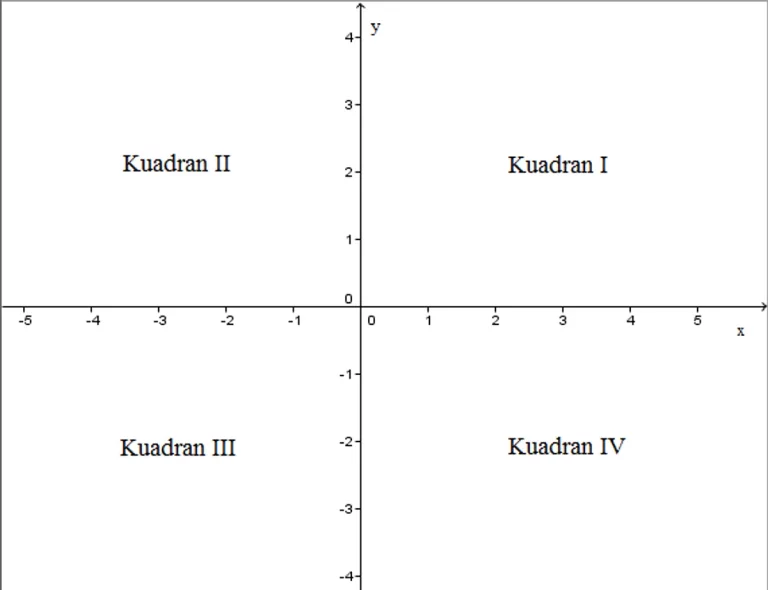
Ketika kita membahas kuadran koordinat kartesius, kita sedang menjelajahi dunia grafik matematis yang bisa memberikan kita wawasan mendalam. Grafik ini terdiri dari empat kuadran yang dipisahkan oleh sumbu-x dan sumbu-y. Mari kita lihat bagaimana kita dapat memahami hasil dan menginterpretasikan grafik ini dengan lebih baik.
Menafsirkan Letak Titik pada Grafik
Titik pada grafik kuadran koordinat adalah representasi visual dari sepasang koordinat . Kuadran pertama memiliki nilai x dan y positif, kuadran kedua memiliki nilai x negatif dan y positif, dan seterusnya. Ini memberi kita dasar yang kuat untuk menganalisis data dan hubungan matematis.
Implikasi Hasil pada Pengambilan Keputusan
Ketika kita mampu menguraikan dan memahami hasil dari grafik kuadran koordinat, kita dapat melihat implikasi yang mungkin terjadi. Misalnya, apakah suatu titik berada pada kuadran yang menunjukkan pertumbuhan atau penurunan? Informasi ini dapat membimbing pengambilan keputusan, baik dalam konteks matematika murni maupun dalam aplikasi dunia nyata. Grafik menjadi alat yang berguna untuk memetakan perubahan dan membuat keputusan yang informasional.
Menyelami Kesalahan yang Sering Terjadi
Seringkali, kesalahan dalam menentukan kuadran berasal dari kebingungan dalam mengidentifikasi sumbu-x dan sumbu-y. Beberapa orang mungkin salah menentukan tanda positif atau negatif pada koordinat. Kesalahan ini bisa mengakibatkan interpretasi yang keliru terhadap data. Penting untuk memeriksa langkah-langkah dengan cermat saat menempatkan suatu titik pada grafik agar hasilnya akurat dan dapat diandalkan.
Menghindari Kesalahan yang Dapat Mempengaruhi Analisis
Kesalahan umum lainnya adalah mengabaikan tanda atau memperhatikan satu sumbu saja. Ini bisa menyebabkan kesalahan besar dalam menentukan kuadran yang benar. Sebuah kesalahan kecil dapat memberikan hasil yang sangat berbeda, mengubah sepenuhnya interpretasi grafik. Oleh karena itu, kritis dalam menilai setiap langkah dan memastikan akurasi dalam penempatan titik pada kuadran.





